TRIGONOMETRIC RATIOS OF COMPOUND ANGLES

About "Trigonometric ratios of compound angles"

Trigonometric ratios of compound angles :

An angle made up of the algebraic sum of two or more angles is called a compound angle.

Here, we are going see the formulas for trigonometric ratios of compound angles. 

sin (A + B)  =  sinA cosB + cosA sinB

sin (A - B)  =  sinA cosB - cosA sinB

cos (A + B)  =  cosA cosB - sinA cosB

cos (A - B)  =  cosA cosB + sinA cosB

tan (A + B)  =  [tanA + tanB] / [1 - tanA tanB]

tan (A - B)  =  [tanA - tanB] / [1 + tanA tanB]

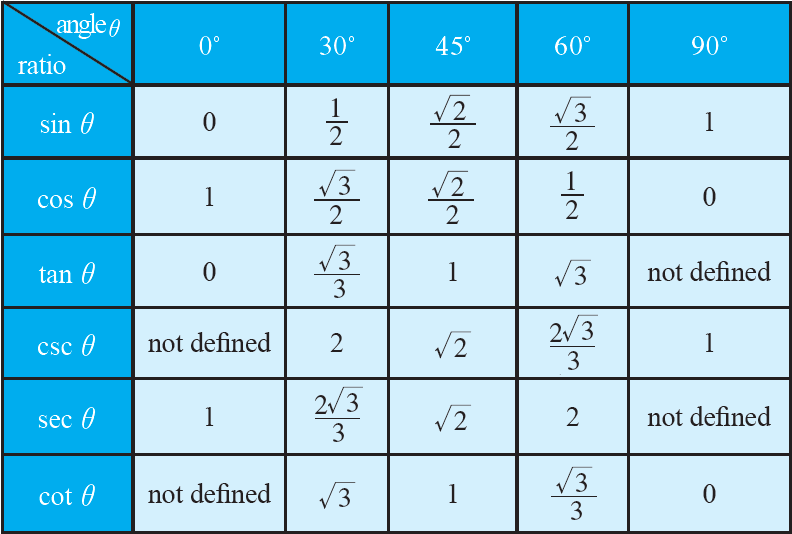
Trigonometric ratio table

From the above table, we can get the values of trigonometric ratios for standard angles such as 0°, 30°, 45°, 60°, 90°

Now, let us look at some practice problems on "Trigonometric ratios of compound angles".

Trigonometric ratios of compound angles - Practice problems

Example 1 :

Find the value of cos15°

Solution :

First, we have to write the given angle 15° in terms of  sum or difference of two standard angles. 

So, we have 15°  =  45° - 30°

cos15°  =  cos (45° - 30°)

cos15°  =  cos45° cos30° + sin45° sin30°

Using the above trigonometric ratio table, we have

cos15°  =  (√2/2) x (√3/2) + (√2/2) x (1/2)

cos15°  =  (√6 / 4)  +  (√2/4)

cos15°  =  (√6 + √2) / 4

Hence, the value of  cos15° is equal to  (√6 + √2) / 4

Let us look at the next problem on "Trigonometric ratios of compound angles"

Example 2 :

Find the value of cos105°

Solution :

First, we have to write the given angle 105° in terms of  sum or difference of two standard angles. 

So, we have 105°  =  60° + 45°

cos105°  =  cos (60° + 45°)

cos105°  =  cos60° cos45° - sin60° sin45°

Using the above trigonometric ratio table, we have

cos105°  =  (1/2) x (√2/2) - (√3/2) x (√2/2)

cos105°  =  (√2 / 4)  -  (√6/4)

cos15°  =  (√2 - √6) / 4

Hence, the value of  cos15° is equal to (√2 - √6) / 4

Let us look at the next problem on "Trigonometric ratios of compound angles"